Wie bestimmt die Produktionstechnologie den Verlauf der Kostenfunktion? Zunächst lässt sich festhalten, dass konstante Skalenerträge den interessanten Grenz- und Sonderfall darstellen. Die Produktionsfunktion ist in diesem Fall eine Gerade durch den Ursprung und die Kostenfunktion ist es ebenfalls. Dieser Zusammenhang wird gleich ausführlicher betrachtet.
Vorher sei noch einmal an die Technik zum Ablesen eines Durchschnittswertes aus einem Diagramm erinnert. Ihr Verständnis ist für die folgende Überlegung unverzichtbar.
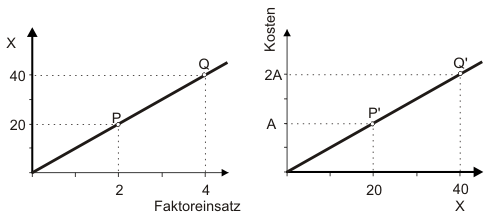
Betrachtet sei der denkbar einfachste Fall (siehe Abbildung 1). Alles ist linear. Eine Verdoppelung der Faktoreinsätze führt zu einer Verdopplung der Produktion. Mit der Verdopplung der Faktoreinsätze verdoppeln sich aber auch die Kosten von A auf 2A, weil die Preise der Faktoren infolge vollkommener Konkurrenz auf den Märkten konstant bleiben. Mit doppelten Kosten wird nun die doppelte Menge hergestellt. Ergo: pro Stück - also im Durchschnitt - bleiben die Kosten konstant. M.a.W.: Die Durchschnitts- oder Stückkosten sind konstant. Die Kostenfunktion muss somit eine Gerade durch den Ursprung sein.
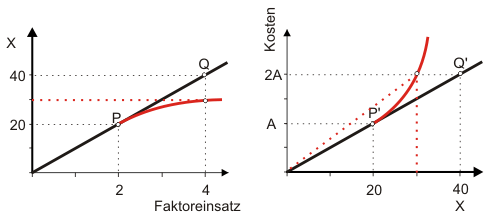
Klicken Sie nun auf Abbildung 1. Sie sehen jetzt eine weitere, rot eingezeichnete Produktionsfunktion. Hier steigt die Produktionsmenge mit dem Faktoreinsatz offensichtlich nur unterproportional an. Während sich die Kosten wieder von A auf 2A verdoppeln, verdoppelt sich die Produktionsmenge nicht. Auf eine produzierte Einheit müssen im Schnitt also höhere Kosten entfallen. Die Durchschnittskosten steigen daher an. Das bedeutet, dass der Winkel im Ursprung, den die rote Hilfsgerade mit der Abszisse bildet, größer sein muss als der Winkel der schwarzen Kostenfunktion mit den konstanten Stückkosten. Der Tangens dieses Winkels zeigt ja die Durchschnittskosten an. Schlussfolgerung: Steigt die Produktionsfunktion unterproportional an, dann muss die Kostenfunktion überproportional ansteigen (und natürlich umgekehrt).
Das war vielleicht verständlich, aber nicht besonders elegant formuliert. Eine Übersetzung in's Ökonomendeutsch würde lauten: "Ist die Skalenelastizität kleiner eins, so steigen die Stückkosten et vice versa." Aus dieser Überlegung folgt unmittelbar ein weiteres wichtiges Resultat: Konstante Skalenerträge haben konstante Grenz- und Durchschnittskosten zur Folge. Das ist ja genau der Spezialfall, der hier in Abbildung 1 dargestellt ist.
Betrachtet sei nun noch ein besonderer Punkt der Produktionsfunktion, von dem aus der Diskussion des Klassischen Ertragsgesetzes bekannt ist, dass er den Faktoreinsatz anzeigt, bei dem der Durchschnittsertrag maximal wird. Bei dieser Produktionsmenge müssen die Durchschnittskosten ihr Minimum haben, denn nirgendwo sonst werden weniger Ressourcen pro Stück verbraucht, fallen also weniger Kosten pro Stück an. Der Punkt P' auf der Kostenfunktion entspricht also dem Punkt P auf der Produktionsfunktion.
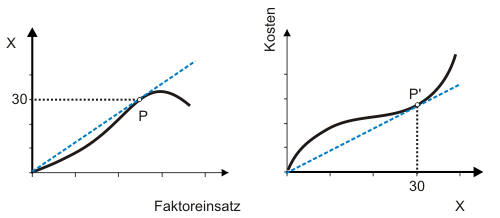
Aus dieser Abbildung kann man übrigens deutlich erkennen, dass die Kostenfunktion nicht die Umkehrfunktion der Produktionsfunktion ist. Dieses Gerücht hält sich hartnäckig. Aber schon allein die Achsenbezeichnungen lassen erkennen, dass es nicht so sein kann.
Allerdings ist es bei der Bestimmung der Kostenfunktion notwendig, Produktionsmengen über den Expansionspfad (die Verbindung aller Minimalkostenkostenkombination) Faktoreinsätze zuzuordnen. Insofern spielt die Umkehrung der Produktionsfunktion schon eine Rolle bei der Ermittlung der Kostenfunktion. Im Zahlenbeispiel zur Theorie der Unternehmung wird dies besonders deutlich (siehe dort den Übergang von d) nach e)).